Sway Bar Link Force Calculator
Trying to see how efficient your sway bar mechanism is? Looking at understanding simple vector forces
when force is applied at different angles? This simple calculator will show how that all adds up. With some
simple math it can all be calculated.
To Find the Force placed on each direction (vertical and horizontal vectors) the calculations are as follows-
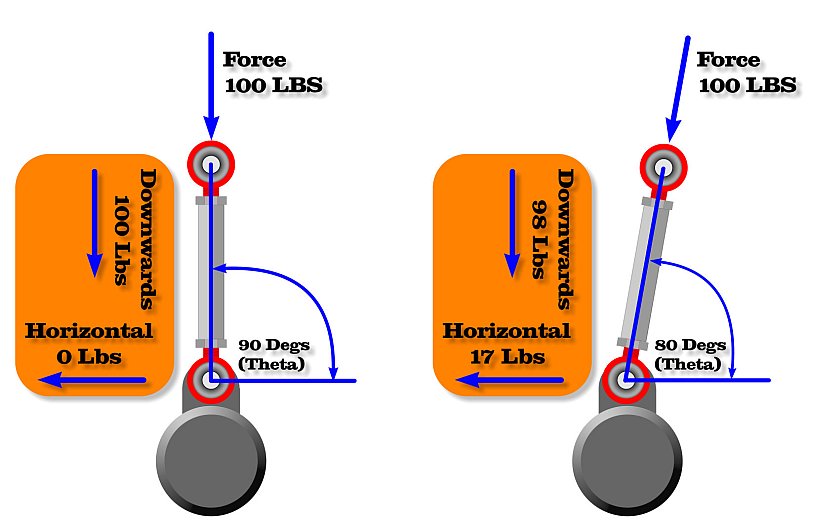
ForceVertical = Force x sin(θ)
ForceHorizontal = Force x cos(θ)
Where-
θ (Theta) = Angle of the bar in degrees
Force = Force along the bar (The type doesn't matter ie, Lbs, Stone, Kg...)
Note : The sine function 'sin()' and cosine 'cos()', in this case must expect
the value in degrees not radians.
What is this used for?
Well it can be used to show the mechanical transfer of force depending on how angled the link bar might be.
If you are running your link bar at extreme angles it will also show how high the force might be in the
horizontal direction which may have undesirable effects such as moving the suspension around. This also
shows the efficiencies of the system, at 90 degrees the system would be very good at transferring the forces
where it should go, however as suspension moves so will the angle of the bar and so will the amount of
forces being put on the Horizontal and Vertical directions.
The picture below shows what we are calculating. It's important to note that the FORCE must be what is
directly inline with the bar, ie, same direction. Sway bar arms are typically examples of this. With the typical
sway bar the angle of the link will change when the suspension is compress and when fully extended.
When all said and done my guess is at rest the link should be vertical as the best starting point (sway bar
arms parallel to suspension), this would be the middle of the road when suspension either compresses or
extends. Yes, I'm learning as I go too. Comments always welcome here! Click the small spark plug in the
very upper right of the page for the comments page.
Still Work in Progress!